Prim's Algorithm은 먼저 다루었던 크루스칼 알고리즘과 같은 대표적인 최소 신장 트리 알고리즘이다.
프림 알고리즘이 크루스칼 알고리즘보다 조금 더 복잡하다.
두 알고리즘 모두 탐욕 알고리즘을 기반으로 하는데,
Kruskal's algorithm은 단순히 가중치를 기준으로 sorting하여 작은 것부터 선택하며 MST를 구하지만,
Prim's algorithm은 특정 정점에서 시작하여, 이 정점에 연결된 가장 작은 가중치의 간선을 선택하며 MST를 구한다.
하나의 정점을 정하고,
이 정점에 연결되어 있는 간선들을 리스트에 담은 후,
이 리스트에서 weight가 가장 작은 간선을 선택하여 cycle이 이루어지지 않는지 확인하고 연결한다.
이 때 간선들을 담는 리스트의 자료형으로 최소힙을 사용하면 좋을 것 같다. ➡️ python의 heapq 라이브러리 사용해보기🤓
그래프는 Kruskal's algorithm때와 같이 아래의 것을 사용한다.
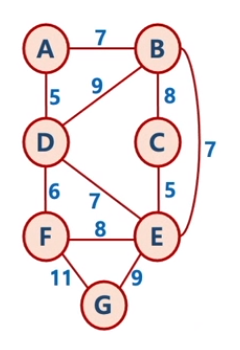
이번에는 그래프를 아래 리스트와 같이 표현한다.
myedges = [
(7, 'A', 'B'), (5, 'A', 'D'),
(8, 'B', 'C'), (9, 'B', 'D'), (7, 'B', 'E'),
(5, 'C', 'E'),
(7, 'D', 'E'), (6, 'D', 'F'),
(8, 'E', 'F'), (9, 'E', 'G'),
(11, 'F', 'G')
]weight와, node1, node2를 튜플로 하여 하나의 edge를 표현하였다.
방향이 없는 그래프이므로 각 edge는 node1, node2 구분 없이 하나만 포함한다.
이 알고리즘에서 사용할 변수로는 크게,
- mst 리스트
- adjacent_edges 딕셔너리
- connected_nodes 리스트
- candiate_edge_list 리스트
가 있다.
1. 우선 adjacent_edges 딕셔너리에는 key로 하나의 정점을, value로는 이 정점이 포함된 간선 리스트를 담아 초기화 한다.
2. 먼저 정해진 하나의 정점은 연결된 것이니 connected_list에 담고, 이 정점이 포함된 adjacent_list[첫 정점]를 후보 리스트(candidate_edge_list)에 담는다.
3. candiate_edge_list는 heap으로 만들어 weight가 작은 것부터 pop 할 수 있도록 한다.
4. 그리고 candidate_edge_list가 빌 때까지,
candiate_edge_list에서 하나씩 pop해서 connected_nodes에 있는 정점과 연결이 안되는 간선이라면 연결한다.
5. 연결할 때는 mst에 append하고, 2번처럼 connected_nodes에 추가하고, candidate_edge_list에 해당 정점의 adjacent_edge를 추가해야 하는데, 이미 연결된 정점과 연결되지 않은 간선만 추가한다.
Code
글로 설명해보니 더 이해하기 어려운 이 과정을 코드로 보자면 아래와 같다.
from collections import defaultdict
from heapq import *
def prim(start_node, edges):
mst = list()
adjacent_edges = defaultdict(list)
for weight, n1, n2 in edges: # adjacent_deges 초기화
# 방향 그래프가 아니기 때문에 두 정점에 모두 추가
adjacent_edges[n1].append((weight, n1, n2))
adjacent_edges[n2].append((weight, n2, n1))
connected_nodes = set(start_node)
candidate_edge_list = adjacent_edges[start_node]
heapify(candidate_edge_list)
while candidate_edge_list:
weight, n1, n2 = heappop(candidate_edge_list)
if n2 not in connected_nodes:
connected_nodes.add(n2)
mst.append((weight, n1, n2))
for edge in adjacent_edges[n2]:
if edge[2] not in connected_nodes: # 이미 연결된 노드에 포함된 간선이 아닐 때
heappush(candidate_edge_list, edge) # candiate에 push
return mstdictionary를 사용할 때 정의되지 않은 key로 접근하여도 기본값이 리턴될 수 있도록 defaultdict를 사용했고,
candidate_edge_list를 최소힙으로 사용하기 위해 heapq를 사용했다.
Result
prim('A', myedges)하여 잘 구현되었는지 확인해본다.
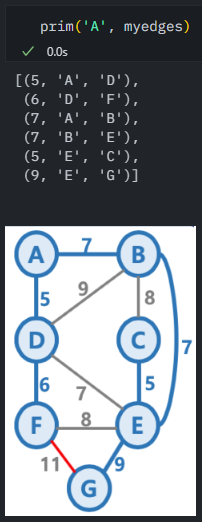
Time Complexity
시간 복잡도는 위에서 설명한 5단계를 기준으로 살펴보자면,
1단계에서는 O(E)만큼의 시간 복잡도가 있을 것이고,
2-3단계에서는 일정한 개수에 대한 처리일 뿐이니 전체 시간 복잡도에 영향이 없을 것이고,
4-5단계의 시간 복잡도가 조금 복잡하다.
최악의 경우에는 모든 간선이 들어가서 모두 반복하여 간선 개수만큼 실행되고, 그러면 최소힙 구조를 사용할 때 O(logN)이 되니, O(ElogE)가 되겠다.
결론적으로 이 알고리즘의 시간 복잡도는 O(ElogE)이다.
'ProblemSolving' 카테고리의 다른 글
| Backtracking with Python (0) | 2023.06.27 |
|---|---|
| Kruskal's Algorithm with Python (0) | 2023.06.23 |
| 패스트캠퍼스 Python 코딩테스트 강의 한 달 후기 (0) | 2023.05.17 |
| 패스트캠퍼스 Python 코딩테스트 강의 4주차 (0) | 2023.05.11 |
| 패스트캠퍼스 Python 코딩테스트 강의 3주차 (0) | 2023.05.07 |



