Backtracking with Python
백트래킹은 문제 해결 기법으로,
제약 조건 만족 문제에서 해를 찾기 위한 전략이다.
고려할 수 있는 모든 경우의 수를 상태 공간 트리(State Space Tree)를 통해 표현하여
각 후보군을 DFS 방식으로 탐색한다.
- Promising: 해당 루트가 조건에 맞는지 검사하는 기법
- Pruning: 조건에 맞지 않으면 제거하고 다른 루트로 바로 넘어가 탐색 시간 절약하는 기법(가지치기)
N Queen 문제
가장 대표적인 백트래킹 문제 유형.
NxN 체스판에 N개의 Queen을 서로 공격할 수 없도록 배치하는 문제
...체스에서 퀸은 가장 강력한 말인데, 수직/수평/대각선으로 이동 및 공격 가능함.
이 체스판 문제를 앞서 말한 대로 상태 공간 트리로 표현하고, Promising 및 Pruning을 하려면 아래와 같이 그릴 수 있다.
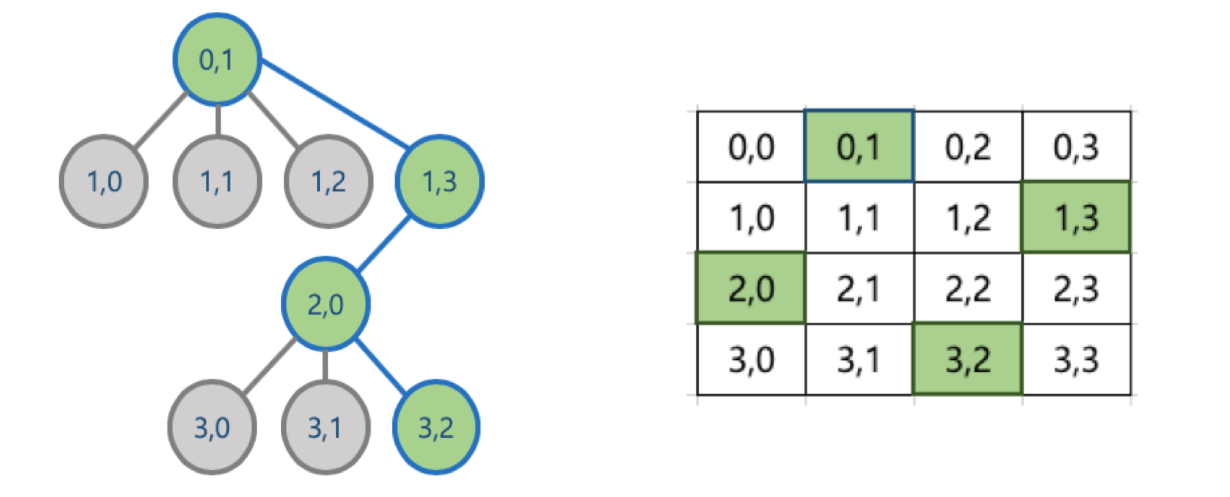
체스판을 좌표로 표현하여 이를 트리로 표현해 본다.
우선 기본적으로 퀸은 수평하게 움직일 수 있기 때문에, 같은 행에는 단 하나의 퀸만 가능하다.
그래서 다음 퀸이 위치할 수도 있는 것이 다음 행이니, 이를 자식 노드에 추가한다...
여기에서 이제 위치하지 못하는 칸은 가지치기, pruning 한다.
이제 조건에 맞는지 체크하는 promising을 확인해 보자.
수직으로 이동이 안되니, 기존 퀸과 열이 같으면 제거된다.
대각선도 이동할 수 없으니, abs(queen_col-1), abs(queen_row-1)의 칸들은 지운다.
어떻게 정답을 저장할 것이냐, 어떻게 경우의 수를 체크할 것이냐가 관건이겠다.
N Queen 문제에서는 0부터 N까지의 모든 행에 Queen이 존재함으로, row는 생략하고 column값만 순차적으로 리스트에 담아 리턴하면 되겠다. 😶🌫️
이를테면, 4x4의 체스판에 결과로 [1, 0, 3, 2]가 리턴된다면, (0,1) (1,0) (2,3) (3,2)에 Queen이 존재한다는 것.
solve_n_queens()는 DFS로 탐색을 하기 때문에 DFS 함수를 먼저 생각해 보자.
DFS(N, 현재 row, 현재 후보 queen, 최종 리스트)를 구현한다.
만약 현재 행이 N이면 current_candidate를 모두 final_result에 넣어 리턴하면 된다.
그렇지 않다면 N번을 반복하여 candidate_col을 모두 체크한다. ➡️ is_available(current_candidate, current_col): current_candidate의 수직에 있는지, 대각선에 있는지 확인한다.
체크한 결과 괜찮다면, 재귀적으로 DFS()에 다음 row를 넣어 호출한다.
그러고 나서 끝을 못 본다면 backtrack 해야 하는데, current_candidate.pop()하여 후보를 빼어냄으로써 백트래킹을 하면 된다.
좀 헷갈린다😣
앞서 말한 candidate_col을 체크하는 is_available() 함수를 보자면,
이미 추가된 candiate와 같은 row에 있지 않은지, abs(candidate-current_col)이 current_row - quene이지 않는지 확인한다.
Code
앞서 말한 내용들이 코드로 구현된 모습을 보자.
def is_available(candidate, current_col): # promissing
current_row = len(candidate)
for queen_row in range(current_row):
if candidate[queen_row] == current_col or abs(candidate[queen_row] - current_col) == current_row - queen_row:
return False
return True
def DFS(N, current_row, current_candidate, final_result):
if current_row == N:
final_result.append(current_candidate[:])
return
for candidate_col in range(N):
if is_available(current_candidate, candidate_col):
current_candidate.append(candidate_col)
DFS(N, current_row + 1, current_candidate, final_result)
current_candidate.pop() # backtrack
def solve_n_queens(N):
final_result = []
DFS(N, 0, [], final_result)
return final_result;
Result
solve_n_queens(4)하여 잘 구현되었는지 확인해 본다.
[[1, 3, 0, 2], [2, 0, 3, 1]]