패스트캠퍼스 Python 코딩테스트 강의 2주차

패스트캠퍼스 Python 코딩테스트 강의 [개발자 취업 합격 패스 with 코딩테스트, 기술면접]를 수강하며 정리한 글입니다🤓
Content
지난주에 수강한 기초 자료구조 배열, 큐, 스택, 링크드리스트에 이어 시간 복잡도가 나온다.
알고리즘 복잡도
다양한 알고리즘들 중 어떤 알고리즘이 더 좋은지 판단하기 위한 복잡도 계산
- 시간 복잡도 (중요)
- 공간 복잡도
시간 복잡도
반복문이 지배함
종류
- Big O 표기법: 최악의 실행 시간 표기
아무리 최악의 상황이어도 이 정도의 성능은 보장한다는 의미를 가져 많이 사용됨
O(1) < O(logN) < O(NlogN) < O(n^2) < O(2^N) < O(N!)
- 오메가 표기법: 최상의 실행 시간 표기
- 세타 표기법: 평균 실행 시간 표기
빅오 표기법으로 간단한 알고리즘을 평가해 보자
1부터 n까지의 합을 구하는 알고리즘 두 개를 예로 들어보자면
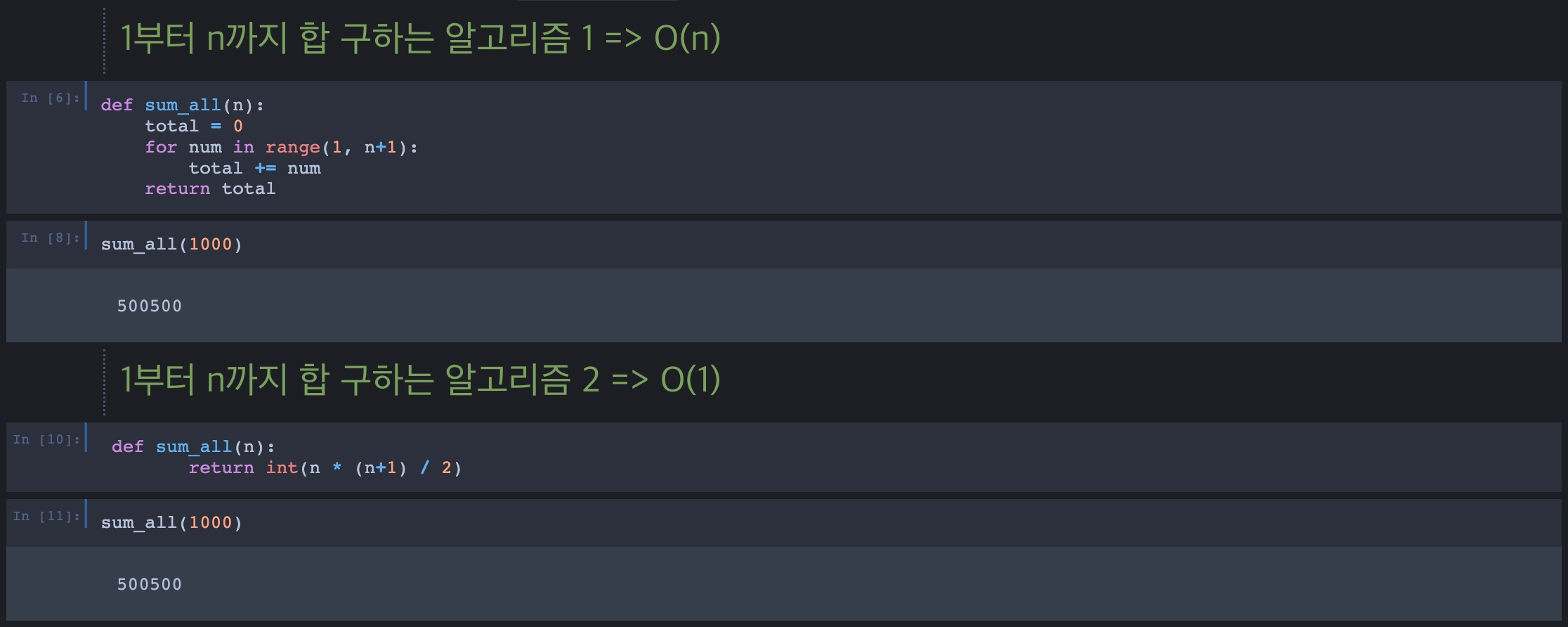
이와 같이 2번 알고리즘이 훨씬 더 좋다고 평가된다
핵심이 되는 것은 반복문!
해쉬 Hash
Key에 Value 저장하는 구조
Key를 통해 데이터를 받아 올 수 있어 속도가 획기적으로 빨라짐
Python의 Dictionary, 블록체인 기술도 해쉬 기능을 확장하였음! 여러모로 많이 사용됨
~용어~
hash: 임의 값을 고정 길이로 변환하는 것
hash table: key값 연산에 의해 직접 접근 가능한 데이터 구조
hashing function: key에 대해 산술 연산하여 위치를 찾을 수 있는 함수
hash value/hash address: key를 해싱 함수로 연산하여 해쉬값을 알아내고, 이를 통해 해쉬테이블에서 key에 대한 데이터를 알아냄
slot: 한 개 데이터를 저장할 수 있는 공간
트리 Tree
자료구조에서 좀 복잡한 것? 하면 생각나는 트리. 잘 알고 있으면 좋다
Node와 Branch를 이용하여 사이클을 이루지 않도록 구상한 데이터 구조
주로 탐색에서 많이 쓰임
이진트리 vs 이진 탐색 트리
이진트리: 노드 최대 Branch가 2인 트리
이진 탐색 트리: 이진 트리인데, 왼쪽 노드는 Parent보다 작은 값, 오른쪽 노드는 Parent보다 큰 값을 가짐
자료 구조 중에서 트리, 트리 중에서 이진 트리, 이진 트리 중에서도 이진 탐색 트리가 많이 쓰이는데
복잡하다는 단점
기본 이진 탐색 트리에 insert와 search 함수를 구현해 봅니다

삭제하는 경우의 케이스는 세 가지가 있는데,
1. child node가 없을 때 (Leaf Node)
2. child node가 1개일 때
3. child node가 2개일 때 (가장 복잡..)
a. 삭제할 Node의 오른쪽 자식 중, 가장 작은 값을 삭제할 Node의 Parent Node가 가리키도록 함
b. 삭제할 Node의 왼쪽 자식 중, 가장 큰 값을 삭제할 Node의 Parent Node가 가리키도록
3번의 a를 한 단계씩 읊어보자면...
- 삭제할 노드의 오른쪽 자식 선택
- 오른쪽 자식의 가장 왼쪽 노드 선택
- 해당 노드를, 삭제할 노드의 Parent Node의 왼쪽 Branch가 가리키게 함
- 해당 노드의 왼쪽 Branch가 삭제할 노드의 왼쪽 노드를 가리키게 함
- 해당 노드의 오른쪽 Branch가 삭제할 노드의 오른쪽 child node를 가리키게 함
- 만약 해당 노드가 오른쪽 child node 가지고 있었을 때는 해당 Node의 본래 Parent Node의 왼쪽 Branch가 해당 오른쪽 child Node를 가리키게 함
...🙄
이런 복잡한 문제를 마주했을 경우 케이스를 세분화하고 해결해 나가면 된다! ➡️ divide and conquer
결국 많이 사용하는 전략은 Divide and Conquer이다.
어떤 복잡한 문제를 마주하더라도, 문제를 잘게 자른 후 하나씩 해결하면 가능함.
그래서 이진탐색 트리의 search, insert, delete까지 구현된 코드는 아래와 같다
class NodeMgmt:
def __init__(self, head):
self.head = head
def insert(self, value):
self.current_node = self.head
while True:
if value < self.current_node.value:
if self.current_node.left != None:
self.current_node = self.current_node.left
else:
self.current_node.left = Node(value)
break
else:
if self.current_node.right != None:
self.current_node = self.current_node.right
else:
self.current_node.right = Node(value)
break
def search(self, value):
self.current_node = self.head
while self.current_node:
if self.current_node.value == value:
return True
elif value < self.current_node.value:
self.current_node = self.current_node.left
else:
self.current_node = self.current_node.right
return False
def delete(self, value):
# 삭제할 Node 탐색
searched = False
self.current_node = self.head
self.parent = self.head
while self.current_node:
if self.current_node.value == value:
searched = True
break
elif value < self.current_node.value:
self.parent = self.current_node
self.current_node = self.current_node.left
else:
self.parent = self.current_node
self.current_node = self.current_node.right
if searched == False:
return False
# case 1: Leaf Node
if self.current_node.left == None and self.current_node.right == None:
if value < self.parent.value:
self.parent.left = None
else:
self.parent.right = None
# case 2: Have 1 child node
elif self.current_node.left != None and self.current_node.right == None:
if value < self.parent.value:
self.parent.left = self.current_node.left
else:
self.parent.right = self.current_node.left
elif self.current_node.left == None and self.current_node.right != None:
if value < self.parent.value:
self.parent.left = self.current_node.right
else:
self.parent.right = self.current_node.right
# case 3: Have 2 child nodes
elif self.current_node.left != None and self.current_node.right != None:
if value < self.parent.value: # case 3-1: 삭제할 Node가 Parent의 왼쪽에 위치, 삭제할 Node의 오른쪽 자식 중 가장 작은 값을 삭제한 Node 자리에 위치
self.change_node = self.current_node.right
self.change_node_parent = self.current_node.right
while self.change_node.left != None:
self.change_node_parent = self.change_node
self.change_node = self.change_node.left
if self.change_node.right != None: # 가장 작은 값 오른쪽에 Child Node가 있을 때
self.change_node_parent.left = self.change_node.right
else:
self.change_node_parent.left = None
self.parent.left = self.change_node # case 3 안 if문에서 유일하게 다른 구문
self.change_node.right = self.change_node.right
self.change_node.left = self.current_node.left
else: # case 3-2: 삭제할 Node가 Parent의 오른쪽에 위치, 삭제할 Node의 오른쪽 자식 중 가장 작은 값을 삭제한 Node 자리에 위치
self.change_node = self.current_node.right
self.change_node_parent = self.current_node.right
while self.change_node.left != None:
self.change_node_parent = self.change_node
self.change_node = self.change_node.left
if self.change_node.right != None:
self.change_node_parent.left = self.change_node.right
else:
self.change_node_parent.left = None
self.parent.right = self.change_node # case 3 안 if문에서 유일하게 다른 구문
self.change_node.left = self.current_node.left
self.change_node.right = self.current_node.right
del self.current_node
return True
이진 탐색 트리가 잘 구현되었는지 테스트하는 코드도 구현해본다
import random
bst_nums = set()
while len(bst_nums) != 100:
bst_nums.add(random.randint(0,999))
head = Node(500)
binary_tree = NodeMgmt(head)
for num in bst_nums:
binary_tree.insert(num)
for num in bst_nums:
if binary_tree.search(num) == False:
print("search failed: ", num)
delete_nums = set() # 중복 막기 위함
bst_nums = list(bst_nums)
while len(delete_nums) != 10 :
delete_nums.add(bst_nums[random.randint(0,99)])
for del_num in delete_nums:
if binary_tree.delete(del_num) == False:
print("delete failed: ", del_num)1-1000의 수 중 100개를 임의 추출하고,
head를 500으로 하여 이진 탐색트리로 insert 한 다음,
이 중 랜덤한 수 10개를 선정해 delete해 보는 코드이다.
실행 시아무런 출력이 없다면 오류가 없다는 뜻이다🥳
Link
https://fastcampus.co.kr/dev_online_devjob
개발자 취업 합격 패스 With 코딩테스트, 기술면접 초격차 패키지 Online. | 패스트캠퍼스
전문가의 코딩테스트 풀이 강의, 기술면접 합격 수준 답안 강의, 네카라쿠배 합격자의 극비 노하우까지 빠짐없이 담았습니다.
fastcampus.co.kr
본 포스팅은 패스트캠퍼스 환급 챌린지 참여를 위해 작성되었습니다.
#패스트캠퍼스 #패캠 #FASTCAMPUS #자바 #자바스크립트 #파이썬 #코딩테스트 #패스트캠퍼스후기 #코딩교육 #코딩자격증